REMINDERS: Answers in red. Solvers (submitted/correct) in blue. (Forgive any omissions, but feel free to inform.) Comments in green. For further elaboration on solutions, please feel free to ask!
- Simplify: (2 + 0 + 2 + 2)2 – (2 – 0 – 2 – 2)2 + 20 – 22 36 – 4 + 20 – 22 = 30. Rita Barger, Amy Ragsdale, Anita Dixon, Jenni Wall
- When could it believably be said that 8 + 8 = 4? (Suspect there may be multiple answers?) ONE ANSWER: Eight hours added to 8:00 is 4:00. (Another involved rolls of toilet paper – creative!) Rita Barger, Jenni Wall, Alexis Avis
- 9,811,438,761 divided by 9 leaves what remainder? 3 Rita Barger, Amy Ragsdale, Anita Dixon, Jenni Wall, Frank Green, Alexis Avis
- A board 2.5 meters long is divided into ten equal pieces. How long – in centimeters – is each piece? 25 (cm). Rita Barger, Amy Ragsdale, Anita Dixon, Jenni Wall, Alexis Avis, Frank Green
- Two different prime numbers are selected at random from among the first ten primes. What is the probability that their sum is 24? (Express your answer as a fraction.) 1/15. (There are 45 different selections. 3 of them have a sum of 24. ) Rita Barger, Anita Dixon, Frank Green
- Too easy? Merry Christmas! 😊
7. Rita Barger, Amy Ragsdale, Anita Dixon, Frank Green, Alexis Avis, Jenni Wall - Find the least common multiple of 10, 15, and 18. 90. Rita Barger, Amy Ragsdale, Anita Dixon, Frank Green, Alexis Avis
- How many distinct rearrangements are there of the word “MATH”? 24. Rita Barger, Anita Dixon
- You have 628 cm. of string, which you may form into either a square or a circle. Which figure will yield the most area? The circle. Rita Barger, Amy Ragsdale, Anita Dixon, Alexis Avis
- The maximum speed of a zebra is 40 mph. IF the zebra could keep up that speed, how long would it take it to run one mile? 1.5 minutes. Rita Barger, Amy Ragsdale, Anita Dixon, Alexis Avis
- How many positive integers less than 124 are divisible by 2, 3, and 5? 4. (30, 60, 90, 120) Rita Barger, Anita Dixon, Alexis Avis
- Find the product of the first five even whole numbers. 0. (0 is the first even whole number.) Rita Barger, Anita Dixon
- Which of the following best describes the GCD of two numbers? a) always even b) always odd c) never prime d) none of these. d. Rita Barger, Anita Dixon, Don Hayes, Frank Green
- There are several combinations of whole numbers whose sum is 12. Find the pair with the greatest product. 6, 6. Rita Barger, Amy Ragsdale, Anita Dixon, Alexis Avis, Frank Green
- Find two examples of numbers that have exactly three factors (no more, no less). The first 3: 4, 9, 25. Rita Barger, Amy Ragsdale, Anita Dixon, Alexis Avis
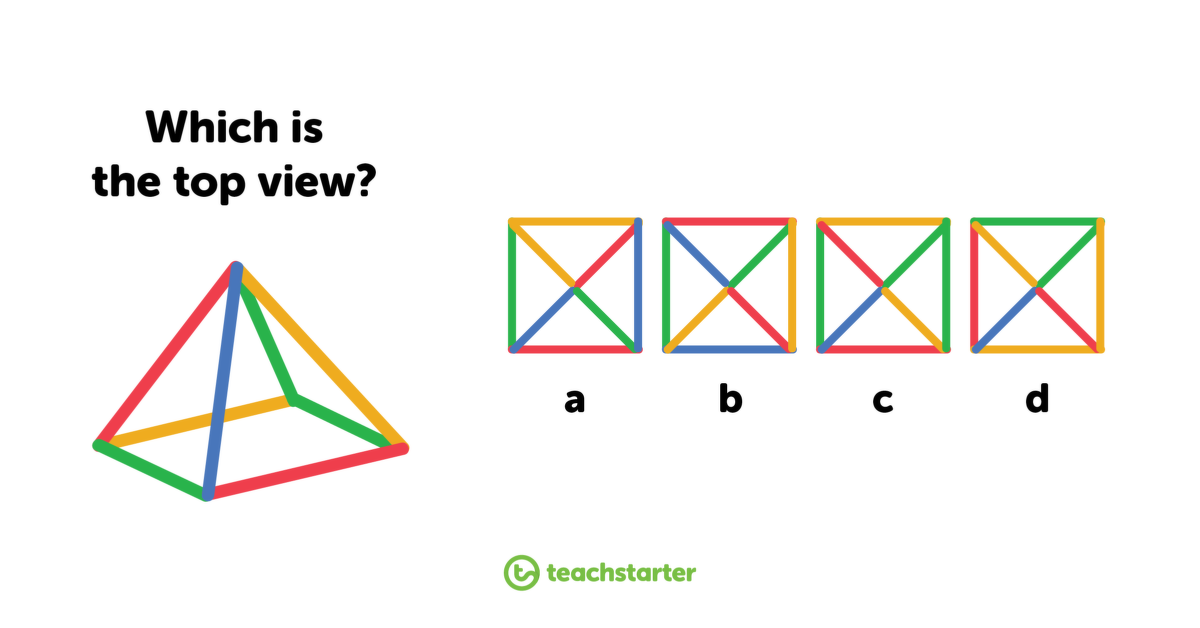c. Rita Barger, Anita Dixon, Alexis Avis
Bonus 1: See #3 above. What slick math tidbit makes this problem easy to solve without paper, pencil, or calculator? The old technique of “casting out 9’s”. (Inquire for further details.) Rita Barger, Amy Ragsdale, Anita Dixon, Alexis Avis
Bonus 2: Square a two-digit number and subtract one. Under what conditions will the result be prime? Never. (Viewed as the difference of two squares, it quickly factors. So it has two factors [and neither can be 1. why?], so it can’t be prime.) Don Hayes
Bonus 3: Write the number (124 – 54) as a product of primes. 7*13*13*17 (the number is 20111, and one could find the answer by trial/error. But it’s easier/luckier to recognize it as a “difference of two squares”, factor it (two steps), and work with smaller numbers.) Rita Barger, Anita Dixon
Bonus 4: See #15. Do you know (or can you deduce) what is true in general about integers with exactly three factors? They are always the squares of primes. (They are not always odd, although 4 is the only exception. [why?]) Full or partial credit to Rita Barger, Amy Ragsdale, Anita Dixon, Alexis Avis
Comments are closed