NOTE: Newest BTs in red, Bonuses in blue, comments in green, updates in purple.
- In 1982, T.R. Benker set a joke-telling record. He told jokes continuously for 1803 minutes. How much longer than one day did he tell jokes?
- The widest street in the world is the Monumental Axis in Brasilia, Brazil. It has 6 lanes and is 0.25 kilometers wide. If 1 meter = 1.1 yards, how wide is the street in feet?
- What is the least common multiple of 54 and 81? How about the greatest common divisor of 16, 41, and 198?
- (A repeat from May ’17) You have 10 consecutive integers. The sum of the first 3 is 39. What is the sum of the last two?
- Variations on a oft-repeated theme: a) Find a proper fraction between 3/7 and 4/9. b) Note that if I just added numerators and denominators, I’d get 7/16. Is 7/16 a solution also?
- Of the first 10 counting numbers, three of them have an odd number of factors. Find the sum of these three numbers.
- Of the first 25 counting numbers, how many of them have an odd number of factors?
- Goldbach’s Conjecture states (in one equivalent variation) that every even integer greater than 2 can be written as the sum of two primes. Verify this is so for the even integers from 10 to 20. (Bonus Bonus: Prove or disprove this Conjecture in general, and A) win an autographed copy of each of my books, and B) make us both famous! 🙂 ).
- If the day before yesterday is the 23rd, what is the day after tomorrow?
- See Pic 1 below. I have one solution for this, but I’m not sure I like it. Can someone else get others?
- See Pic 2 below (and clarification there). I’m kinda doubting the ‘90% fail answer’. If you remember your order of operations, this should be a piece of cake!
- Find the largest fraction that a) has a denominator of 17, and b) when added to 1/3, keeps a sum less than 1.
- If a certain book is 4th from the left on a bookshelf, and also 6th from the right on the same shelf, how many books are on the shelf?
- (Repeat?) How can you throw a ball as hard as you can and have it come back to you, even if it doesn’t bounce off anything? There is nothing attached to it, and no one else catches or throws it back to you.
- What is impossible to hold for an hour, even though it hardly weighs anything?
- How many times can you take 3 from 96?
BONUS #1: (Ongoing) What’s the last digit (units place) of the product of the first 100 primes?
BONUS #2: What else do you notice about the numbers you found in #7?
CREATIVITY BONUS #3: Make as long of a sentence as you can (at least 5 words?) where every word starts with the same letter. (LOTS of ‘right’ answers, of course!! Should be fun!) Ongoing Update: As of May 16, we have one entry with 10 words, and another with 20! Any length (>5) is fine!! Join the fun!
BONUS #4: The grades on six tests are all on a 0 – 100 scale, inclusive. If the average for the six tests is 93, what’s the lowest possible grade on any one test (in order to maintain the 93 average)?
Pic 1: For #10 above.
Pic 2: For #11 above.
(NOTE: Let’s assume there is a + sign at the end of 1st 2 rows. Thanks to Amy Ragsdale for noticing!)
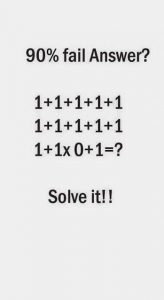
Comments are closed